The Moreau-Yosida regularization is a technique used to approximate lower semicontinuous functions by Lipschitz functions. An important application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the narrow convergence in the space of probability measures.
Definitions
Let  be a metric space, and let
be a metric space, and let  denotes the collection of probability measures on
denotes the collection of probability measures on  .
.  is said to be a Polish space if it is complete and separable.
is said to be a Polish space if it is complete and separable.
A function ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) is said to be proper [1] if it is not identically equal to
is said to be proper [1] if it is not identically equal to  , that is, if there exists
, that is, if there exists  such that
such that  . The domain
. The domain  of
of  is the set
is the set
 .
.
For a given function ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) and
and  , its Moreau-Yosida regularization [1]
, its Moreau-Yosida regularization [1] ![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9) is given by
is given by
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)
The distance term  may often be raised to a positive exponent
may often be raised to a positive exponent  , in particular
, in particular  . For example, when
. For example, when  is a Hilbert space [2] [3],
is a Hilbert space [2] [3],  is taken to be
is taken to be
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+{\frac {k}{2}}\|x-y\|^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cf1385a2f69fa59b328558c773e4c8cbd5379e)
This particular variant in a Hilbert space setting is explored in more detail below.
The dependence on the parameter  may also be written instead as
may also be written instead as
![{\displaystyle \inf \limits _{y\in X}\left[g(y)+{\frac {1}{\tau }}d(x,y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582441b7aa0292a3c7e74c281b1fb36106aeac96)
for  .
.
Note that
![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc) .
.
Examples
- If
 , then by definition
, then by definition  is constant and
is constant and  .
.
- If
 is not proper, then
is not proper, then  for all
for all  .
.
Take  . If
. If  is finite-valued and differentiable, we can write down an expression for
is finite-valued and differentiable, we can write down an expression for  . For a fixed
. For a fixed  , the map
, the map  is continuous everywhere and differentiable everywhere except for when
is continuous everywhere and differentiable everywhere except for when  , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for
, where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for  : find the critical points of
: find the critical points of  and take the infimum of
and take the infimum of  evaluated at the critical points. One of these values will always be the original function
evaluated at the critical points. One of these values will always be the original function  evaluated at
evaluated at  , since this corresponds to the critical point
, since this corresponds to the critical point  for
for  .
.
- Let
 . Then
. Then

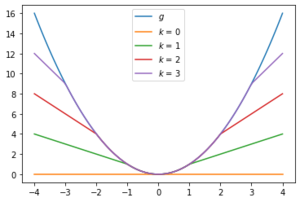
Plot of

and

for

.
Approximating Lower Semicontinuous Functions by Lipschitz Functions
Proposition. [1][4] Let  be a Polish space and let
be a Polish space and let ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) .
.
- If
 is proper and bounded below, so is
is proper and bounded below, so is  . Furthermore,
. Furthermore,  is Lipschitz continuous for all
is Lipschitz continuous for all  .
.
- If, in addition,
 is lower semicontinuous, then
is lower semicontinuous, then  for all
for all  .
.
- In this case,
 is continuous and bounded and
is continuous and bounded and  for all
for all  .
.
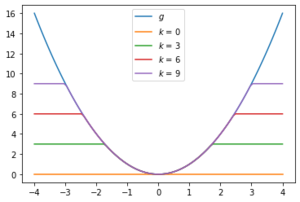
Plot of

and

for

.
Proof.
- Since
 is proper, there exists
is proper, there exists  such that
such that  . Then for any
. Then for any 

Thus  is proper and bounded below. Next, for a fixed
is proper and bounded below. Next, for a fixed  , let
, let  . Then as
. Then as
 ,
,
the family  is uniformly Lipschitz and hence equicontinuous. Thus
is uniformly Lipschitz and hence equicontinuous. Thus  is Lipschitz continuous.
is Lipschitz continuous.
- Suppose that
 is also lower semicontinuous. Note that for all
is also lower semicontinuous. Note that for all  ,
,  . Thus it suffices to show that
. Thus it suffices to show that  . This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that
. This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that  . By definition of infimum, for each
. By definition of infimum, for each  there exists
there exists  such that
such that
 .
.
Then
![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)
 is bounded below by assumption, while the only way
is bounded below by assumption, while the only way  to be finite in the limit is for
to be finite in the limit is for  to vanish in the limit. Thus
to vanish in the limit. Thus  converges to
converges to  in
in  , and by lower semicontinuity of
, and by lower semicontinuity of  ,
,
![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18) .
.
- By definition,
 . Since
. Since  for all
for all  ,
,  for all
for all  .
.
Portmanteau Theorem
Theorem (Portmanteau). [1] [4] Let  be a Polish space, and let
be a Polish space, and let ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) be lower semicontinuous and bounded below. Then the functional
be lower semicontinuous and bounded below. Then the functional  is lower semicontinuous with respect to narrow convergence in
is lower semicontinuous with respect to narrow convergence in  , that is
, that is
 .
.
Proof. By the Moreau-Yosida approximation, for all  ,
,
 .
.
Taking  , Fatou's Lemma ensures that
, Fatou's Lemma ensures that
 .
.
Etymology of Portmanteau Theorem
The curious epithet attached to the above theorem is due to Billingsley [5], with a citation to a Jean-Pierre Portmanteau's Espoir pour l'ensemble vide? published in Annales de l'Université de Felletin in 1915. This is believed to be a fictional citation made as a play on words [6].
- The publication date is far too early; Kolmogorov's probability axioms were published in 1933. [7]
- Felletin is a small town in central France with no university, and there is no record of a Jean-Pierre Portmanteau aside from this citation.
- "Espoir pour l'ensemble vide" translates to "hope for the empty set" (translation was by Google, please confirm or amend if you speak French!)
Generalizations
The Moreau-Yosida regularization is a specific case of a type of convolution, and many of the above results follow from this generalization. This material is adapted from Bauschke-Combettes Chapter 12 [2], where the setting is over a Hilbert space instead of a more general Polish space.
Let  be a Hilbert space, and let
be a Hilbert space, and let ![{\displaystyle f,g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bb6747a456f1d3093f1701de6e22a5aba35cb1) . The infimal convolution or epi-sum
. The infimal convolution or epi-sum ![{\displaystyle f\,\square \,g:{\mathcal {H}}\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a440689324748d01a4799137be6803d361e999b8) of
of  and
and  is
is
![{\displaystyle (f\,\square \,g)(x):=\inf \limits _{y\in {\mathcal {H}}}\left[f(y)+g(x-y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba5cf937bf606019fe7a2544a62aa94784545533) .
.
 is said to be exact at a point
is said to be exact at a point  if this infimum is attained.
if this infimum is attained.  is said to be exact if it is exact at every point of its domain, and in this case it is denoted by
is said to be exact if it is exact at every point of its domain, and in this case it is denoted by  .
.
Remark. Bauschke-Combettes uses a box with a dot in the middle for  to be exact. Due to technical difficulties, we will use
to be exact. Due to technical difficulties, we will use  instead.
instead.
For an example, let  be nonempty. Then
be nonempty. Then  is exact, and
is exact, and  .
.
Proposition. Let ![{\displaystyle g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc944df555284c429809b500dda2b6ab6efc81f) be proper,
be proper,  , and for
, and for  , let
, let ![{\displaystyle g_{k}:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5782b22092d0f649b11da86ab8caa96a31a0ee6f) be given by
be given by
 .
.
Then the following hold for all  and
and  :
:
 ,
,- for
 ,
,  ,
,
 ,
, as
as  , and
, and is bounded above on every ball in
is bounded above on every ball in  .
.
Remark. The convention given above differs slightly from Bauschke-Combettes to fit the convention in this article. The Moreau-Yosida regularization is the special case where  , and is called the Pasch-Hausdorff Envelope in Bauschke-Combettes.
, and is called the Pasch-Hausdorff Envelope in Bauschke-Combettes.
Proposition. Let ![{\displaystyle g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc944df555284c429809b500dda2b6ab6efc81f) be lower semicontinuous and convex, let
be lower semicontinuous and convex, let  , and let
, and let  . Then the infimal convolution
. Then the infimal convolution  is convex, proper, continuous, and exact. Moreover, for every
is convex, proper, continuous, and exact. Moreover, for every  , the infimum
, the infimum
![{\displaystyle g_{k}(x)=\inf \limits _{y\in {\mathcal {H}}}\left[g(y)+{\frac {k}{p}}\|x-y\|^{p}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3971541254290c55489de326e7b2bbfcb42e4ce)
is uniquely attained.
References
- ↑ 1.0 1.1 1.2 1.3 Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ 2.0 2.1 Bauschke, Heinz H. and Patrick L. Combettes. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed. Ch. 12. Springer, 2017.
- ↑ Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. Gradient Flows in Metric Spaces and in the Space of Probability Measures. Ch. 3.1. Birkhäuser, 2005.
- ↑ 4.0 4.1 Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.
- ↑ Billingsley, Patrick. Convergence of Probability Measures, 2nd Ed. John Wiley & Sons, Inc. 1999.
- ↑ Pagès, Gilles. Numerical Probability: An Introduction with Applications to Finance. Ch. 4.1. Springer, 2018.
- ↑ Kolmogorov, Andrey (1950) [1933]. Foundations of the theory of probability. New York, USA: Chelsea Publishing Company.



![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)







![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)




![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+{\frac {k}{2}}\|x-y\|^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cf1385a2f69fa59b328558c773e4c8cbd5379e)

![{\displaystyle \inf \limits _{y\in X}\left[g(y)+{\frac {1}{\tau }}d(x,y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582441b7aa0292a3c7e74c281b1fb36106aeac96)

![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc)





































![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)




![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18)







![{\displaystyle f,g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bb6747a456f1d3093f1701de6e22a5aba35cb1)
![{\displaystyle f\,\square \,g:{\mathcal {H}}\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a440689324748d01a4799137be6803d361e999b8)

![{\displaystyle (f\,\square \,g)(x):=\inf \limits _{y\in {\mathcal {H}}}\left[f(y)+g(x-y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba5cf937bf606019fe7a2544a62aa94784545533)






![{\displaystyle g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc944df555284c429809b500dda2b6ab6efc81f)


![{\displaystyle g_{k}:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5782b22092d0f649b11da86ab8caa96a31a0ee6f)









![{\displaystyle g_{k}(x)=\inf \limits _{y\in {\mathcal {H}}}\left[g(y)+{\frac {k}{p}}\|x-y\|^{p}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3971541254290c55489de326e7b2bbfcb42e4ce)