(to be filled in)
Motivation
(to be filled in)
Definitions
Let  be a metric space. A function
be a metric space. A function ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) is said to be proper if it is not identically equal to
is said to be proper if it is not identically equal to  , that is, if there exists
, that is, if there exists  such that
such that  .
.
For a given function ![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd) and
and  , its Moreau-Yosida regularization
, its Moreau-Yosida regularization ![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9) is given by
is given by
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)
Note that
![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc) .
.
Examples
- If
 , then by definition
, then by definition  is constant and
is constant and  .
.
- If
 is not proper, then
is not proper, then  for all
for all  .
.
Take  . If
. If  is finite-valued and differentiable, we can explicitly write down
is finite-valued and differentiable, we can explicitly write down  . Then for a fixed
. Then for a fixed  , the map
, the map  is continuous everywhere and differentiable everywhere except for when
is continuous everywhere and differentiable everywhere except for when  , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for
, where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for  : find the critical points of
: find the critical points of  and take the infimum of
and take the infimum of  evaluated at the critical points. One of these values will always be the original function
evaluated at the critical points. One of these values will always be the original function  evaluated at
evaluated at  , since this corresponds to the critical point
, since this corresponds to the critical point  for
for  .
.
- Let
 . Then
. Then

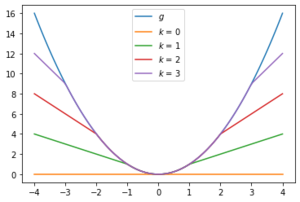
Plot of

and

for

.
Results
Proposition. [1][2]
- If
 is proper and bounded below, so is
is proper and bounded below, so is  . Furthermore,
. Furthermore,  is continuous for all
is continuous for all  .
.
- If, in addition,
 is lower semicontinuous, then
is lower semicontinuous, then  for all
for all  .
.
- In this case,
 is continuous and bounded and
is continuous and bounded and  for all
for all  .
.
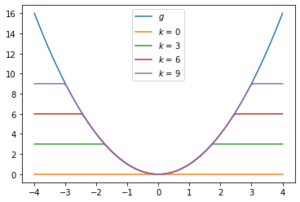
Plot of

and

for

.
Proof.
- Since
 is proper, there exists
is proper, there exists  such that
such that  . Then for any
. Then for any 

Thus  is proper and bounded below. Next, for a fixed
is proper and bounded below. Next, for a fixed  , let
, let  . Then as
. Then as
 ,
,
the family  is uniformly Lipschitz and hence equicontinuous. Thus
is uniformly Lipschitz and hence equicontinuous. Thus  is Lipschitz continuous.
is Lipschitz continuous.
- Suppose that
 is also lower semicontinuous. Note that for all
is also lower semicontinuous. Note that for all  ,
,  . Thus it suffices to show that
. Thus it suffices to show that  . This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that
. This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that  . By definition of infimum, for each
. By definition of infimum, for each  there exists
there exists  such that
such that
 .
.
Then
![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)
 is bounded below by assumption, while the only way
is bounded below by assumption, while the only way  is finite in the limit is for
is finite in the limit is for  to go to zero. Thus
to go to zero. Thus  converges to
converges to  in
in  , and by lower semicontinuity of
, and by lower semicontinuity of  ,
,
![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18) .
.
- By definition,
 . Since
. Since  for all
for all  ,
,  for all
for all  .
.
References
- ↑ Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.

![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)




![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)
![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc)







































![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)





![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18)
