The Moreau-Yosida Regularization: Difference between revisions
mNo edit summary |
(added the origin of the name portmanteau, added internal and external links) |
||
| Line 1: | Line 1: | ||
The '''Moreau-Yosida regularization''' is a technique used to approximate lower semicontinuous functions by Lipschitz functions. The main application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the narrow topology in the space of probability measures. | The '''Moreau-Yosida regularization''' is a technique used to approximate [[lower semicontinuous functions]] by Lipschitz functions. The main application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the narrow topology in the space of probability measures. | ||
==Definitions== | ==Definitions== | ||
| Line 57: | Line 57: | ||
==Portmanteau Theorem== | ==Portmanteau Theorem== | ||
'''Theorem (Portmanteau).''' <ref name="OT" /> Let <math>(X,d)</math> be a Polish space, and let <math>g : X \to (-\infty,+\infty]</math> be lower semicontinuous and bounded below. Then the functional <math>\mu \mapsto \int_X g \, \mathrm{d}\mu</math> is lower semicontinuous with respect to narrow convergence in <math>\mathcal{P}(X)</math>, that is | '''Theorem (Portmanteau).''' <ref name="OT" /> <ref name="S"/> Let <math>(X,d)</math> be a Polish space, and let <math>g : X \to (-\infty,+\infty]</math> be lower semicontinuous and bounded below. Then the functional <math>\mu \mapsto \int_X g \, \mathrm{d}\mu</math> is lower semicontinuous with respect to narrow convergence in <math>\mathcal{P}(X)</math>, that is | ||
<math> \mu_n \to \mu \text{ narrowly} \Longrightarrow \liminf\limits_{n \to \infty} \int_X g_n \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | <math> \mu_n \to \mu \text{ narrowly} \Longrightarrow \liminf\limits_{n \to \infty} \int_X g_n \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | ||
| Line 65: | Line 65: | ||
:<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{n \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu_n = \int_X g_k \wedge k \, \mathrm{d}\mu </math>. | :<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{n \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu_n = \int_X g_k \wedge k \, \mathrm{d}\mu </math>. | ||
Taking <math>k \to \infty</math>, Fatou's | Taking <math>k \to \infty</math>, [[Fatou's Lemma]] ensures that | ||
:<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{k \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | :<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{k \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | ||
==The Mysterious Etymology of Portmanteau== | ==The Mysterious Etymology of Portmanteau== | ||
( | The curious epithet attached to the above theorem is due to Billingsley <ref name="B"/>, with a citation to a Jean-Pierre Portmanteau's ''Espoir pour l'ensemble vide?'' published in ''Annales de l'Université de Felletin'' in 1915. This is believed to be a fictional citation made as a play on words <ref name="Pages"/>. | ||
* The publication date is far too early; Kolmogorov's probability axioms were published in 1933. <ref name="Kolmogorov"/> | |||
* [https://en.wikipedia.org/wiki/Felletin Felletin] is a small town in central France with no university, and there is no record of a Jean-Pierre Portmanteau aside from this citation. | |||
* "Espoir pour l'ensemble vide" translates to "hope for the empty set" (translation was by Google, please confirm or amend if you speak French!) | |||
==References== | ==References== | ||
| Line 80: | Line 83: | ||
<ref name="BC">Bauschke, Heinz H. and Patrick L. Combettes. ''Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed.'' Ch. 12. Springer, 2017.</ref> | <ref name="BC">Bauschke, Heinz H. and Patrick L. Combettes. ''Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed.'' Ch. 12. Springer, 2017.</ref> | ||
<ref name="S">Santambrogio, Filippo. ''Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling'' Ch. 1.1. Birkhäuser, 2015.</ref> | <ref name="S">Santambrogio, Filippo. ''Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling'' Ch. 1.1. Birkhäuser, 2015.</ref> | ||
<ref name="B">Billingsley, Patrick. ''Convergence of Probability Measures, 2nd Ed.'' John Wiley & Sons, Inc. 1999. </ref> | |||
<ref name="Pages">Pagès, Gilles. ''Numerical Probability: An Introduction with Applications to Finance.'' Ch. 4.1. Springer, 2018.</ref> | |||
<ref name="Kolmogorov">Kolmogorov, Andrey (1950) [1933]. Foundations of the theory of probability. New York, USA: Chelsea Publishing Company.</ref> | |||
<!-- | |||
<ref name="P">https://math.stackexchange.com/questions/43747/where-did-the-portmanteau-theorem-get-its-name | |||
<ref name="Q">https://www.quora.com/What-is-the-Portmanteau-theorem-And-who-knows-the-reason-for-that-name | |||
--> | |||
</references> | </references> | ||
Revision as of 02:55, 12 February 2022
The Moreau-Yosida regularization is a technique used to approximate lower semicontinuous functions by Lipschitz functions. The main application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the narrow topology in the space of probability measures.
Definitions
Let be a metric space, and let denotes the collection of probability measures on . is said to be a Polish space if it is complete and separable.
A function is said to be proper if it is not identically equal to , that is, if there exists such that .
For a given function and , its Moreau-Yosida regularization is given by
The distance term may often be raised to a positive exponent. For example, when is a Hilbert space [1] [2], is taken to be
Note that
- .
Examples
- If , then by definition is constant and .
- If is not proper, then for all .
Take . If is finite-valued and differentiable, we can explicitly write down . Then for a fixed , the map is continuous everywhere and differentiable everywhere except for when , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for : find the critical points of and take the infimum of evaluated at the critical points. One of these values will always be the original function evaluated at , since this corresponds to the critical point for .
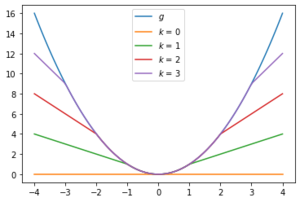
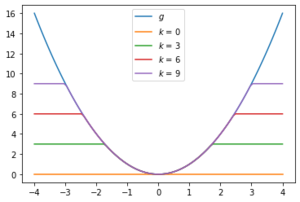
- Let . Then
Approximating Lower Semicontinuous Functions by Lipschitz Functions
Proposition. [3][4] Let be a Polish space and let .
- If is proper and bounded below, so is . Furthermore, is continuous for all .
- If, in addition, is lower semicontinuous, then for all .
- In this case, is continuous and bounded and for all .
Proof.
- Since is proper, there exists such that . Then for any
Thus is proper and bounded below. Next, for a fixed , let . Then as
- ,
the family is uniformly Lipschitz and hence equicontinuous. Thus is Lipschitz continuous.
- Suppose that is also lower semicontinuous. Note that for all , . Thus it suffices to show that . This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that . By definition of infimum, for each there exists such that
- .
Then
is bounded below by assumption, while the only way is finite in the limit is for to go to zero. Thus converges to in , and by lower semicontinuity of ,
- .
- By definition, . Since for all , for all .
Portmanteau Theorem
Theorem (Portmanteau). [3] [4] Let be a Polish space, and let be lower semicontinuous and bounded below. Then the functional is lower semicontinuous with respect to narrow convergence in , that is
.
Proof. By the Moreau-Yosida approximation, for all ,
- .
Taking , Fatou's Lemma ensures that
- .
The Mysterious Etymology of Portmanteau
The curious epithet attached to the above theorem is due to Billingsley [5], with a citation to a Jean-Pierre Portmanteau's Espoir pour l'ensemble vide? published in Annales de l'Université de Felletin in 1915. This is believed to be a fictional citation made as a play on words [6].
- The publication date is far too early; Kolmogorov's probability axioms were published in 1933. [7]
- Felletin is a small town in central France with no university, and there is no record of a Jean-Pierre Portmanteau aside from this citation.
- "Espoir pour l'ensemble vide" translates to "hope for the empty set" (translation was by Google, please confirm or amend if you speak French!)
References
- ↑ Bauschke, Heinz H. and Patrick L. Combettes. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed. Ch. 12. Springer, 2017.
- ↑ Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. Gradient Flows in Metric Spaces and in the Space of Probability Measures. Ch. 3.1. Birkhäuser, 2005.
- ↑ 3.0 3.1 Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ 4.0 4.1 Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.
- ↑ Billingsley, Patrick. Convergence of Probability Measures, 2nd Ed. John Wiley & Sons, Inc. 1999.
- ↑ Pagès, Gilles. Numerical Probability: An Introduction with Applications to Finance. Ch. 4.1. Springer, 2018.
- ↑ Kolmogorov, Andrey (1950) [1933]. Foundations of the theory of probability. New York, USA: Chelsea Publishing Company.



![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)




![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)


![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+k\|x-y\|^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a65d7289ce32f930246fe926a3b06afc67710e75)
![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc)




































![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)




![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18)





