The Moreau-Yosida Regularization: Difference between revisions
(added an example) |
(added a picture, still need to figure out how to add a caption and to position it properly) |
||
| Line 11: | Line 11: | ||
:<math>g_k(x) := \inf\limits_{y \in X} \left[ g(y) + k d(x,y) \right].</math> | :<math>g_k(x) := \inf\limits_{y \in X} \left[ g(y) + k d(x,y) \right].</math> | ||
==Examples== | ==Examples== | ||
| Line 23: | Line 20: | ||
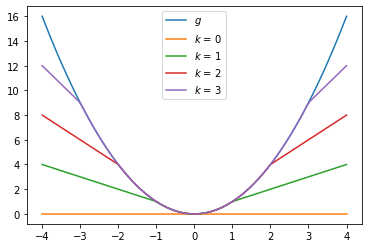
:<math>g_k(x) = \min \left\{ x^2 , \frac{k^2}{2} + k \left| x \pm \frac{k}{2} \right| \right\}.</math> | :<math>g_k(x) = \min \left\{ x^2 , \frac{k^2}{2} + k \left| x \pm \frac{k}{2} \right| \right\}.</math> | ||
[[File:Ex 1.png|alt=Plot of <math>g(x) = x^2</math> and <math>g_k(x)</math> for <math>k = 0, 1, 2, 3</math>.]] | |||
==Results== | ==Results== | ||
Revision as of 01:08, 9 February 2022
(to be filled in)
Motivation
(to be filled in)
Definitions
Let be a metric space. A function is said to be proper if it is not identically equal to , that is, if there exists such that .
For a given function and , its Moreau-Yosida regularization is given by
Examples
- If , then by definition is constant and .
- If is not proper, then for all .
Take . If is finite-valued and differentiable, we can explicitly write down . Then for a fixed , the map is continuous everywhere and differentiable everywhere except for when , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for : find the critical points of and take the infimum of evaluated at the critical points. One of these values will always be the original function evaluated at , since this corresponds to the critical point for .
- Let . Then
Results
Proposition. [1]
- If is proper and bounded below, so is . Furthermore, is continuous for all .
- If, in addition, is lower semicontinuous, then for all .
- In this case, is continuous and bounded and for all .
References
Possible list of references, will fix accordingly
Bauschke-Combette Ch 12.[2]; Santambrogio (6)[3]; Ambrosio-Gigli-Savare (59-61)[4]
- ↑ Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ Bauschke, Heinz H. and Patrick L. Combettes. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed. Ch. 12. Springer, 2017.
- ↑ Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.
- ↑ Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. Gradient Flows in Metric Spaces and in the Space of Probability Measures. Ch. 3.1. Birkhäuser, 2005.

![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)




![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)