The Moreau-Yosida Regularization: Difference between revisions
(added proof to main result) |
m (→Results) |
||
| Line 40: | Line 40: | ||
the family <math> \{ h_{k,y} \}_{y \in X} </math> is uniformly Lipschitz and hence equicontinuous. Thus <math>g_k = \inf\limits_{y \in Y} h_{k,y}</math> is Lipschitz continuous. | the family <math> \{ h_{k,y} \}_{y \in X} </math> is uniformly Lipschitz and hence equicontinuous. Thus <math>g_k = \inf\limits_{y \in Y} h_{k,y}</math> is Lipschitz continuous. | ||
* Suppose that <math>g</math> is also lower semicontinuous. Note that for all <math>k_1 \leq k_2</math>, <math>g_{k_1}(x) \leq g_{k_2}(x) \leq g(x)</math>. Thus it suffices to show that <math>\liminf\limits_{k \to \infty} g_k(x) \geq g(x)</math>. This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that <math>\liminf\limits_{k \to \infty} g_k(x) < +\infty</math>. By definition of infimum, for each <math>k \in \mathbb{N}</math> there exists <math>y_k \in X</math> such that | * Suppose that <math>g</math> is also lower semicontinuous. Note that for all <math>k_1 \leq k_2</math>, <math>g_{k_1}(x) \leq g_{k_2}(x) \leq g(x)</math>. Thus it suffices to show that <math>\liminf\limits_{k \to \infty} g_k(x) \geq g(x)</math>. This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that <math>\liminf\limits_{k \to \infty} g_k(x) < +\infty</math>. By definition of infimum, for each <math>k \in \mathbb{N}</math> there exists <math>y_k \in X</math> such that | ||
:<math>g(y_k) + k d(x,y_k) \leq g_k(x) + \frac{1}{k}</math>. Then | |||
:<math>g(y_k) + k d(x,y_k) \leq g_k(x) + \frac{1}{k}</math>. | |||
Then | |||
:<math>+\infty > \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right].</math> | :<math>+\infty > \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right].</math> | ||
<math>g(y_k)</math> is bounded below by assumption, while the only way <math>kd(x,y_k)</math> is finite in the limit is for <math>d(x,y_k)</math> to go to zero. Thus <math>y_k</math> converges to <math>x</math> in <math>X</math>, and by lower semicontinuity of <math>g</math>, | <math>g(y_k)</math> is bounded below by assumption, while the only way <math>kd(x,y_k)</math> is finite in the limit is for <math>d(x,y_k)</math> to go to zero. Thus <math>y_k</math> converges to <math>x</math> in <math>X</math>, and by lower semicontinuity of <math>g</math>, | ||
:<math> \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right] \geq g(x) </math>. | :<math> \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right] \geq g(x) </math>. | ||
* By definition, <math>g_k \wedge k \in C_b(X)</math>. Since <math>g_k(x) \nearrow g(x)</math> for all <math>x \in X</math>, <math>g_k(x) \wedge k \nearrow g(x)</math> for all <math>x \in X</math>. | * By definition, <math>g_k \wedge k \in C_b(X)</math>. Since <math>g_k(x) \nearrow g(x)</math> for all <math>x \in X</math>, <math>g_k(x) \wedge k \nearrow g(x)</math> for all <math>x \in X</math>. | ||
Revision as of 04:28, 9 February 2022
(to be filled in)
Motivation
(to be filled in)
Definitions
Let be a metric space. A function is said to be proper if it is not identically equal to , that is, if there exists such that .
For a given function and , its Moreau-Yosida regularization is given by
Note that
- .
Examples
- If , then by definition is constant and .
- If is not proper, then for all .
Take . If is finite-valued and differentiable, we can explicitly write down . Then for a fixed , the map is continuous everywhere and differentiable everywhere except for when , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for : find the critical points of and take the infimum of evaluated at the critical points. One of these values will always be the original function evaluated at , since this corresponds to the critical point for .
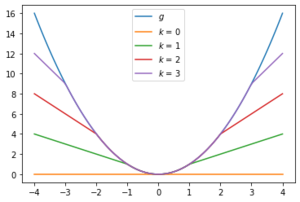
- Let . Then
Results
- If is proper and bounded below, so is . Furthermore, is continuous for all .
- If, in addition, is lower semicontinuous, then for all .
- In this case, is continuous and bounded and for all .
Proof.
- Since is proper, there exists such that . Then for any
Thus is proper and bounded below. Next, for a fixed , let . Then as
- ,
the family is uniformly Lipschitz and hence equicontinuous. Thus is Lipschitz continuous.
- Suppose that is also lower semicontinuous. Note that for all , . Thus it suffices to show that . This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that . By definition of infimum, for each there exists such that
- .
Then
is bounded below by assumption, while the only way is finite in the limit is for to go to zero. Thus converges to in , and by lower semicontinuity of ,
- .
- By definition, . Since for all , for all .
References
Possible list of references, will fix accordingly
Bauschke-Combette Ch 12.[3]; Santambrogio (6)[2]; Ambrosio-Gigli-Savare (59-61)[4]
- ↑ Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ 2.0 2.1 Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.
- ↑ Bauschke, Heinz H. and Patrick L. Combettes. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed. Ch. 12. Springer, 2017.
- ↑ Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. Gradient Flows in Metric Spaces and in the Space of Probability Measures. Ch. 3.1. Birkhäuser, 2005.

![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)




![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)
![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc)



































![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)





![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18)
