The Moreau-Yosida Regularization: Difference between revisions
(added potential list of references, added definition of proper and Moreau-Yosida regularization) |
No edit summary |
||
| (31 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The '''Moreau-Yosida regularization''' is a technique used to approximate [[lower semicontinuous functions]] by [https://en.wikipedia.org/wiki/Lipschitz_continuity Lipschitz functions]. An important application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the [[Convergence of Measures and Metrizability#Narrow Convergence|narrow convergence]] in the space of [https://en.wikipedia.org/wiki/Probability_measure probability measures]. | |||
== | ==Definitions== | ||
(to be | Let <math>(X,d)</math> be a [https://en.wikipedia.org/wiki/Metric_space metric space], and let <math>\mathcal{P}(X)</math> denotes the collection of probability measures on <math>X</math>. <math>(X,d)</math> is said to be a '''Polish space''' if it is [https://en.wikipedia.org/wiki/Complete_metric_space complete] and [https://en.wikipedia.org/wiki/Separable_space separable]. | ||
A function <math>g : X \to (-\infty,+\infty]</math> is said to be '''proper''' <ref name="OT"/> if it is not identically equal to <math>+\infty</math>, that is, if there exists <math>x \in X</math> such that <math>g(x) < +\infty</math>. The '''domain''' <math>D(g)</math> of <math>g</math> is the set | |||
:<math> D(g) := \{ x \in X | g(x) < +\infty \} </math>. | |||
For a given function <math>g : X \to (-\infty,+\infty]</math> and <math>k \geq 0</math>, its '''Moreau-Yosida regularization''' <ref name="OT"/> <math>g_k : X \to [-\infty,+\infty]</math> is given by | |||
<math>g_k(x) := \inf\limits_{y \in X} \left[ g(y) + k d(x,y) \right].</math> | |||
The distance term <math>d(x,y)</math> may often be raised to a positive exponent <math>p</math>, in particular <math>p = 2</math>. For example, when <math>X</math> is a [https://en.wikipedia.org/wiki/Hilbert_space Hilbert space] <ref name="BC"/> <ref name="AGS"/>, <math>g_k</math> is taken to be | |||
<math>g_k(x) := \inf\limits_{y \in X} \left[ g(y) + \frac{k}{2} \| x - y \|^2 \right].</math> | |||
This particular variant in a Hilbert space setting is explored in more detail below. | |||
The dependence on the parameter <math>k</math> may also be written instead as | |||
:<math> \inf\limits_{y \in X} \left[ g(y) + \frac{1}{\tau} d(x,y) \right] </math> | |||
for <math>\tau \in (0,+\infty)</math>. | |||
Note that | |||
:<math>g_k(x) = \inf\limits_{y \in X} \left[ g(y) + k d(x,y) \right] \leq g(x) + k d(x,x) = g(x)</math>. | |||
==Examples== | ==Examples== | ||
(to be | * If <math>k = 0</math>, then by definition <math>g_0</math> is constant and <math>g_0 \equiv \inf\limits_{y \in X} g(y)</math>. | ||
* If <math>g</math> is ''not'' proper, then <math>g_k = +\infty</math> for all <math>k \geq 0</math>. | |||
Take <math>(X,d) := (\mathbb{R},|\cdot|)</math>. If <math>g</math> is finite-valued and differentiable, we can write down an expression for <math>g_k</math>. For a fixed <math>x \in \mathbb{R}</math>, the map <math>g_{k,x} : y \mapsto g(y) + k|x - y|</math> is continuous everywhere and differentiable everywhere except for when <math>y = x</math>, where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for <math>g_k(x)</math>: find the critical points of <math>g_{k,x}</math> and take the infimum of <math>g_{k,x}</math> evaluated at the critical points. One of these values will always be the original function <math>g</math> evaluated at <math>x</math>, since this corresponds to the critical point <math>y = x</math> for <math>g_{k,x}</math>. | |||
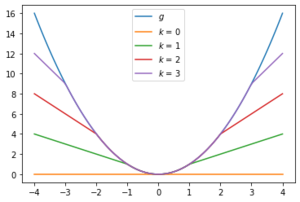
* Let <math>g(x) := x^2</math>. Then | |||
:<math>g_k(x) = \min \left\{ x^2 , \frac{k^2}{2} + k \left| x \pm \frac{k}{2} \right| \right\}.</math> | |||
[[File:Ex 1.png|300px|thumb|Plot of <math>g(x) = x^2</math> and <math>g_k(x)</math> for <math>k = 0, 1, 2, 3</math>.]] | |||
==Approximating Lower Semicontinuous Functions by Lipschitz Functions== | |||
'''Proposition.''' <ref name="OT"/><ref name="S"/> Let <math>(X,d)</math> be a Polish space and let <math>g : X \to (-\infty,+\infty]</math>. | |||
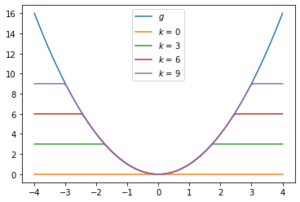
* If <math>g</math> is proper and bounded below, so is <math>g_k</math>. Furthermore, <math>g_k</math> is Lipschitz continuous for all <math>k \geq 0</math>. | |||
* If, in addition, <math>g</math> is lower semicontinuous, then <math>g_k(x) \nearrow g(x)</math> for all <math>x \in X</math>. | |||
* In this case, <math>g_k \wedge k := \min(g_k,k)</math> is continuous and bounded and <math>g_k(x) \wedge k \nearrow g(x)</math> for all <math>x \in X</math>. | |||
[[File:Ex 2.png|300px|thumb|Plot of <math>g(x) = x^2</math> and <math>g_k(x) \wedge k</math> for <math>k = 0, 3, 6, 9</math>.]] | |||
'''Proof.''' | |||
* Since <math>g</math> is proper, there exists <math>y_0 \in X</math> such that <math>g(y_0) < +\infty</math>. Then for any <math>x \in X</math> | |||
:<math> -\infty < \inf\limits_{y \in Y} g(y) \leq g_k(x) \leq g(y_0) + k d(x,y_0) < +\infty .</math> | |||
Thus <math>g_k</math> is proper and bounded below. Next, for a fixed <math>y \in X</math>, let <math>h_{k,y}(x) := g(y) + d(x,y)</math>. Then as | |||
:<math> h_{k,y}(x_1) - h_{k,y}(x_2) = k d(x_1,y) - k d(x_2,y) \leq k d(x_1,x_2) </math> , | |||
the family <math> \{ h_{k,y} \}_{y \in X} </math> is uniformly Lipschitz and hence equicontinuous. Thus <math>g_k = \inf\limits_{y \in Y} h_{k,y}</math> is Lipschitz continuous. | |||
* Suppose that <math>g</math> is also lower semicontinuous. Note that for all <math>k_1 \leq k_2</math>, <math>g_{k_1}(x) \leq g_{k_2}(x) \leq g(x)</math>. Thus it suffices to show that <math>\liminf\limits_{k \to \infty} g_k(x) \geq g(x)</math>. This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that <math>\liminf\limits_{k \to \infty} g_k(x) < +\infty</math>. By definition of infimum, for each <math>k \in \mathbb{N}</math> there exists <math>y_k \in X</math> such that | |||
:<math>g(y_k) + k d(x,y_k) \leq g_k(x) + \frac{1}{k}</math>. | |||
Then | |||
:<math>+\infty > \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right].</math> | |||
<math>g(y_k)</math> is bounded below by assumption, while the only way <math>kd(x,y_k)</math> to be finite in the limit is for <math>d(x,y_k)</math> to vanish in the limit. Thus <math>y_k</math> converges to <math>x</math> in <math>X</math>, and by lower semicontinuity of <math>g</math>, | |||
:<math> \liminf\limits_{k \to \infty} g_k(x) \geq \liminf\limits_{k \to \infty} \left[ g(y_k) + k d(x,y_k) \right] \geq g(x) </math>. | |||
* By definition, <math>g_k \wedge k \in C_b(X)</math>. Since <math>g_k(x) \nearrow g(x)</math> for all <math>x \in X</math>, <math>g_k(x) \wedge k \nearrow g(x)</math> for all <math>x \in X</math>. | |||
==Portmanteau Theorem== | |||
'''Theorem (Portmanteau).''' <ref name="OT"/> <ref name="S"/> Let <math>(X,d)</math> be a Polish space, and let <math>g : X \to (-\infty,+\infty]</math> be lower semicontinuous and bounded below. Then the functional <math>\mu \mapsto \int_X g \, \mathrm{d}\mu</math> is lower semicontinuous with respect to [[Convergence of Measures and Metrizability#Narrow Convergence|narrow convergence]] in <math>\mathcal{P}(X)</math>, that is | |||
<math> \mu_n \to \mu \text{ narrowly} \Longrightarrow \liminf\limits_{n \to \infty} \int_X g_n \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | |||
'''Proof.''' By the Moreau-Yosida approximation, for all <math>k \geq 0</math>, | |||
:<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{n \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu_n = \int_X g_k \wedge k \, \mathrm{d}\mu </math>. | |||
Taking <math>k \to \infty</math>, [[Fatou's Lemma]] ensures that | |||
:<math>\liminf\limits_{n \to \infty} \int_X g \, \mathrm{d} \mu_n \geq \liminf\limits_{k \to \infty} \int_X g_k \wedge k \, \mathrm{d}\mu \geq \int_X g \, \mathrm{d}\mu </math>. | |||
==Etymology of Portmanteau Theorem== | |||
The curious epithet attached to the above theorem is due to [https://en.wikipedia.org/wiki/Patrick_Billingsley Billingsley] <ref name="Billingsley"/>, with a citation to a Jean-Pierre Portmanteau's ''Espoir pour l'ensemble vide?'' published in ''Annales de l'Université de Felletin'' in 1915. This is believed to be a fictional citation made as a play on words <ref name="Pages"/>. | |||
* The publication date is far too early; [https://en.wikipedia.org/wiki/Probability_axioms Kolmogorov's probability axioms] were published in 1933. <ref name="Kolmogorov"/> | |||
* [https://en.wikipedia.org/wiki/Felletin Felletin] is a small town in central France with no university, and there is no record of a Jean-Pierre Portmanteau aside from this citation. | |||
* "Espoir pour l'ensemble vide" translates to "hope for the empty set" (translation was by Google, please confirm or amend if you speak French!) | |||
==Generalizations== | |||
The Moreau-Yosida regularization is a specific case of a type of convolution, and many of the above results follow from this generalization. This material is adapted from Bauschke-Combettes Chapter 12 <ref name="BC"/>, where the setting is over a Hilbert space instead of a more general Polish space. | |||
Let <math>\mathcal{H}</math> be a Hilbert space, and let <math>f , g : \mathcal{H} \to (-\infty,+\infty]</math>. The '''infimal convolution''' or '''epi-sum''' <math>f \, \square \, g : \mathcal{H} \to [-\infty,+\infty]</math> of <math>f</math> and <math>g</math> is | |||
<math> (f \, \square \, g)(x) := \inf\limits_{y \in \mathcal{H}} \left[ f(y) + g(x-y) \right] </math>. | |||
<math>f \, \square \, g</math> is said to be '''exact''' at a point <math>x \in \mathcal{H}</math> if this infimum is attained. <math>f \, \square \, g</math> is said to be exact if it is exact at every point of its domain, and in this case it is denoted by <math>f \, \dot{\square} \, g</math>. | |||
'''Remark.''' Bauschke-Combettes uses a box with a dot in the middle for <math>f \, \square \, g</math> to be exact. Due to technical difficulties, we will use <math>f \, \dot{\square} \, g</math> instead. | |||
For an example, let <math>A, B \subseteq \mathcal{H}</math> be nonempty. Then <math>\chi_A \, \square \, \chi_B</math> is exact, and <math>\chi_A \, \dot{\square} \, \chi_B = \chi_{A + B}</math>. | |||
'''Proposition.''' Let <math>g : \mathcal{H} \to (-\infty,+\infty]</math> be proper, <math>p \in [1,+\infty)</math>, and for <math>k \in (0,+\infty)</math>, let <math>g_k : \mathcal{H} \to (-\infty,+\infty]</math> be given by | |||
:<math> g_k := g \, \square \, \left( \frac{k}{p} \| \cdot \|^p \right) </math>. | |||
Then the following hold for all <math>k \in (0,+\infty)</math> and <math>x \in \mathcal{H}</math>: | |||
* <math>D(g_k) = \mathcal{H}</math>, | |||
* for <math>0 < k_1 \leq k_2 < +\infty</math>, <math>\inf\limits_{y \in \mathcal{H}} g(y) \leq g_{k_1}(x) \leq g_{k_2}(x) \leq g(x)</math>, | |||
* <math>\inf\limits_{x \in \mathcal{H}} g_k(x) = \inf\limits_{x \in \mathcal{H}} g(x)</math>, | |||
* <math>g_k(x) \searrow \inf\limits_{y \in \mathcal{H}} g(y)</math> as <math>k \downarrow 0</math>, and | |||
* <math>g_k</math> is bounded above on every ball in <math>\mathcal{H}</math>. | |||
'''Remark.''' The convention given above differs slightly from Bauschke-Combettes to fit the convention in this article. The Moreau-Yosida regularization is the special case where <math>p = 1</math>, and is called the '''Pasch-Hausdorff Envelope''' in Bauschke-Combettes. | |||
'''Proposition.''' Let <math>g : \mathcal{H} \to (-\infty,+\infty]</math> be lower semicontinuous and convex, let <math>k \in (0,+\infty)</math>, and let <math>p \in (1,+\infty)</math>. Then the infimal convolution <math>g_k</math> is convex, proper, continuous, and exact. Moreover, for every <math>x \in \mathcal{H}</math>, the infimum | |||
:<math>g_k(x) = \inf\limits_{y \in \mathcal{H}} \left[ g(y) + \frac{k}{p} \| x - y \|^p \right]</math> | |||
is uniquely attained. | |||
==References== | ==References== | ||
Bauschke-Combette Ch 12.<ref name="BC" />; Santambrogio (6)<ref name="S" />; Ambrosio-Gigli-Savare (59-61)<ref name="AGS" /> | <!--Bauschke-Combette Ch 12.<ref name="BC"/>; Santambrogio (6)<ref name="S" />; Ambrosio-Gigli-Savare (59-61)<ref name="AGS" />--> | ||
<references> | <references> | ||
<ref name="AGS">Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. ''Gradient Flows in Metric Spaces and in the Space of Probability Measures.'' Ch. 3.1. Birkhäuser, 2005.</ref> | |||
<ref name="Billingsley">Billingsley, Patrick. ''Convergence of Probability Measures, 2nd Ed.'' John Wiley & Sons, Inc. 1999. </ref> | |||
<ref name="BC">Bauschke, Heinz H. and Patrick L. Combettes. ''Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed.'' Ch. 12. Springer, 2017.</ref> | <ref name="BC">Bauschke, Heinz H. and Patrick L. Combettes. ''Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed.'' Ch. 12. Springer, 2017.</ref> | ||
<ref name="Kolmogorov">Kolmogorov, Andrey (1950) [1933]. Foundations of the theory of probability. New York, USA: Chelsea Publishing Company.</ref> | |||
<ref name="Pages">Pagès, Gilles. ''Numerical Probability: An Introduction with Applications to Finance.'' Ch. 4.1. Springer, 2018.</ref> | |||
<ref name="OT">Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.</ref> | |||
<ref name="S">Santambrogio, Filippo. ''Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling'' Ch. 1.1. Birkhäuser, 2015.</ref> | <ref name="S">Santambrogio, Filippo. ''Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling'' Ch. 1.1. Birkhäuser, 2015.</ref> | ||
<ref name=" | <!-- | ||
<ref name="P">https://math.stackexchange.com/questions/43747/where-did-the-portmanteau-theorem-get-its-name | |||
<ref name="Q">https://www.quora.com/What-is-the-Portmanteau-theorem-And-who-knows-the-reason-for-that-name | |||
--> | |||
</references> | </references> | ||
Latest revision as of 20:02, 23 February 2022
The Moreau-Yosida regularization is a technique used to approximate lower semicontinuous functions by Lipschitz functions. An important application of this result is to prove Portmanteau's Theorem, which states that integration against a lower semicontinuous and bounded below function is lower semicontinuous with respect to the narrow convergence in the space of probability measures.
Definitions
Let be a metric space, and let denotes the collection of probability measures on . is said to be a Polish space if it is complete and separable.
A function is said to be proper [1] if it is not identically equal to , that is, if there exists such that . The domain of is the set
- .
For a given function and , its Moreau-Yosida regularization [1] is given by
The distance term may often be raised to a positive exponent , in particular . For example, when is a Hilbert space [2] [3], is taken to be
This particular variant in a Hilbert space setting is explored in more detail below.
The dependence on the parameter may also be written instead as
for .
Note that
- .
Examples
- If , then by definition is constant and .
- If is not proper, then for all .
Take . If is finite-valued and differentiable, we can write down an expression for . For a fixed , the map is continuous everywhere and differentiable everywhere except for when , where the derivative does not exist due to the absolute value. Thus we can apply standard optimization techniques from Calculus to solve for : find the critical points of and take the infimum of evaluated at the critical points. One of these values will always be the original function evaluated at , since this corresponds to the critical point for .
- Let . Then
Approximating Lower Semicontinuous Functions by Lipschitz Functions
Proposition. [1][4] Let be a Polish space and let .
- If is proper and bounded below, so is . Furthermore, is Lipschitz continuous for all .
- If, in addition, is lower semicontinuous, then for all .
- In this case, is continuous and bounded and for all .
Proof.
- Since is proper, there exists such that . Then for any
Thus is proper and bounded below. Next, for a fixed , let . Then as
- ,
the family is uniformly Lipschitz and hence equicontinuous. Thus is Lipschitz continuous.
- Suppose that is also lower semicontinuous. Note that for all , . Thus it suffices to show that . This inequality is automatically satisfied when the left hand side is infinite, so without loss of generality assume that . By definition of infimum, for each there exists such that
- .
Then
is bounded below by assumption, while the only way to be finite in the limit is for to vanish in the limit. Thus converges to in , and by lower semicontinuity of ,
- .
- By definition, . Since for all , for all .
Portmanteau Theorem
Theorem (Portmanteau). [1] [4] Let be a Polish space, and let be lower semicontinuous and bounded below. Then the functional is lower semicontinuous with respect to narrow convergence in , that is
.
Proof. By the Moreau-Yosida approximation, for all ,
- .
Taking , Fatou's Lemma ensures that
- .
Etymology of Portmanteau Theorem
The curious epithet attached to the above theorem is due to Billingsley [5], with a citation to a Jean-Pierre Portmanteau's Espoir pour l'ensemble vide? published in Annales de l'Université de Felletin in 1915. This is believed to be a fictional citation made as a play on words [6].
- The publication date is far too early; Kolmogorov's probability axioms were published in 1933. [7]
- Felletin is a small town in central France with no university, and there is no record of a Jean-Pierre Portmanteau aside from this citation.
- "Espoir pour l'ensemble vide" translates to "hope for the empty set" (translation was by Google, please confirm or amend if you speak French!)
Generalizations
The Moreau-Yosida regularization is a specific case of a type of convolution, and many of the above results follow from this generalization. This material is adapted from Bauschke-Combettes Chapter 12 [2], where the setting is over a Hilbert space instead of a more general Polish space.
Let be a Hilbert space, and let . The infimal convolution or epi-sum of and is
.
is said to be exact at a point if this infimum is attained. is said to be exact if it is exact at every point of its domain, and in this case it is denoted by .
Remark. Bauschke-Combettes uses a box with a dot in the middle for to be exact. Due to technical difficulties, we will use instead.
For an example, let be nonempty. Then is exact, and .
Proposition. Let be proper, , and for , let be given by
- .
Then the following hold for all and :
- ,
- for , ,
- ,
- as , and
- is bounded above on every ball in .
Remark. The convention given above differs slightly from Bauschke-Combettes to fit the convention in this article. The Moreau-Yosida regularization is the special case where , and is called the Pasch-Hausdorff Envelope in Bauschke-Combettes.
Proposition. Let be lower semicontinuous and convex, let , and let . Then the infimal convolution is convex, proper, continuous, and exact. Moreover, for every , the infimum
is uniquely attained.
References
- ↑ 1.0 1.1 1.2 1.3 Craig, Katy C. Lower Semicontinuity in the Narrow Topology. Math 260J. Univ. of Ca. at Santa Barbara. Winter 2022.
- ↑ 2.0 2.1 Bauschke, Heinz H. and Patrick L. Combettes. Convex Analysis and Monotone Operator Theory in Hilbert Spaces, 2nd Ed. Ch. 12. Springer, 2017.
- ↑ Ambrosio, Luigi, Nicola Gigli, and Giuseppe Savaré. Gradient Flows in Metric Spaces and in the Space of Probability Measures. Ch. 3.1. Birkhäuser, 2005.
- ↑ 4.0 4.1 Santambrogio, Filippo. Optimal Transport for Applied Mathematicians: Calculus of Variations, PDEs, and Modeling Ch. 1.1. Birkhäuser, 2015.
- ↑ Billingsley, Patrick. Convergence of Probability Measures, 2nd Ed. John Wiley & Sons, Inc. 1999.
- ↑ Pagès, Gilles. Numerical Probability: An Introduction with Applications to Finance. Ch. 4.1. Springer, 2018.
- ↑ Kolmogorov, Andrey (1950) [1933]. Foundations of the theory of probability. New York, USA: Chelsea Publishing Company.



![{\displaystyle g:X\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb30feface8bba531b0a2ad5b5dffc066ed4acbd)







![{\displaystyle g_{k}:X\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62b2ac0cccbf31ee661e3683c88a306dd393fda9)
![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22a6e02a5f403ff1a143b2dce1719ad675b26942)




![{\displaystyle g_{k}(x):=\inf \limits _{y\in X}\left[g(y)+{\frac {k}{2}}\|x-y\|^{2}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25cf1385a2f69fa59b328558c773e4c8cbd5379e)

![{\displaystyle \inf \limits _{y\in X}\left[g(y)+{\frac {1}{\tau }}d(x,y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582441b7aa0292a3c7e74c281b1fb36106aeac96)

![{\displaystyle g_{k}(x)=\inf \limits _{y\in X}\left[g(y)+kd(x,y)\right]\leq g(x)+kd(x,x)=g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a8f1cb49687f58c965329359e7600db6c847cbc)



































![{\displaystyle +\infty >\liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e5aa798fdcf7e963d899e10c682925747d8e02)




![{\displaystyle \liminf \limits _{k\to \infty }g_{k}(x)\geq \liminf \limits _{k\to \infty }\left[g(y_{k})+kd(x,y_{k})\right]\geq g(x)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f86ba72ccc928cdc1f3cef48ccfda7bbcc502f18)







![{\displaystyle f,g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91bb6747a456f1d3093f1701de6e22a5aba35cb1)
![{\displaystyle f\,\square \,g:{\mathcal {H}}\to [-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a440689324748d01a4799137be6803d361e999b8)

![{\displaystyle (f\,\square \,g)(x):=\inf \limits _{y\in {\mathcal {H}}}\left[f(y)+g(x-y)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba5cf937bf606019fe7a2544a62aa94784545533)






![{\displaystyle g:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cc944df555284c429809b500dda2b6ab6efc81f)


![{\displaystyle g_{k}:{\mathcal {H}}\to (-\infty ,+\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5782b22092d0f649b11da86ab8caa96a31a0ee6f)









![{\displaystyle g_{k}(x)=\inf \limits _{y\in {\mathcal {H}}}\left[g(y)+{\frac {k}{p}}\|x-y\|^{p}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c3971541254290c55489de326e7b2bbfcb42e4ce)