Semidiscrete Optimal Transport: Difference between revisions
Andrewgracyk (talk | contribs) No edit summary |
m (Removed protection from "Semidiscrete Optimal Transport") |
||
| (104 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
Semidiscrete optimal transport refers to situations in optimal transport where two input measures are considered, and one measure is a discrete measure and the other one is continuous. Hence, because only one of the two measures is discrete, we arrive at the appropriate name "semidiscrete." | Semidiscrete optimal transport refers to situations in optimal transport where two input measures are considered, and one measure is a discrete measure and the other one is absolutely continuous with respect to Lebesgue measure.<ref name="Peyré and Cuturi"/> Hence, because only one of the two measures is discrete, we arrive at the appropriate name "semidiscrete." | ||
== Formulation of the | |||
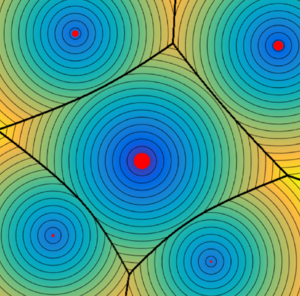
[[File:Voronoi_Cells.png|300px|thumb|right|Voronoi Cells. These partitions of the plane are Voronoi cells, which are used in the semidiscrete dual optimal transport problem. The cell structures are determined by the cost function used, here being the Euclidean metric. The bold black lines represent the cell structure.<ref name="Peyré and Cuturi"/> ]] | |||
== Formulation of the semidiscrete dual problem == | |||
In particular, we will examine semidiscrete optimal transport in the case of the dual problem. The general dual problem for continuous measures can be stated as | In particular, we will examine semidiscrete optimal transport in the case of the dual problem. The general dual problem for continuous measures can be stated as | ||
<math display="block"> \max_{(\ | <math display="block"> \max_{(\psi, \varphi) \in R(c)} \Big\{ \int_X \psi d\mu + \int_Y \varphi d\nu \Big\} </math><ref name="Santambrogio"/> | ||
where <math> \mu, \nu </math> denote probability measures on domains <math> X, Y </math> respectively, and <math> c(x,y) </math> is a cost function defined over <math> X \times Y </math>. <math> R(c) </math> denotes the set of possible dual potentials, and the condition <math> \varphi(x) + \psi(y) \leq c(x,y) </math> is satisfied. It should also be noted that <math> \mu </math> has a density such that <math> \mu = f(x)dx </math>. Now, we would like to extend this notion of the dual problem to the semidiscrete case. Such a case can be reformulated as | |||
<math display="block"> \max_{\varphi \in \R^m} \Big\{ \mathcal{E}(\varphi) = \int_X \varphi^c d\mu + \sum_j \varphi_j b_j \Big\}. </math> | |||
Aside from using a discrete measure in place of what was originally a continuous one, there are a few other notable distinctions within this reformulation. The first is that <math> \varphi^c </math> denotes the c-transform of <math> \varphi </math>. The c-transform can be defined as <math> \varphi^c(x) := \inf_j \{ c(x,y_j) - \varphi_j \} </math>. <math> \varphi_j </math> is used to denote <math> \varphi(y_j) </math>. Furthermore, we note that our original measure <math> \nu </math> is a sum of Dirac masses evaluated at locations <math> y_j </math> with weights <math> b_j </math>, i.e., <math> \nu = \sum_{j=1}^{N} b_j \delta_{y_j} </math>. | |||
== Voronoi cells decomposition == | |||
Now, we will establish the notion of Voronoi cells. The Voronoi cells refer to a special subset of <math> X </math>, and the reason we are interested in such a subset is because we can use the Voronoi cells to find the regions that are sent to each <math> y_j </math>. In particular, if we denote the set of Voronoi cells as <math> V_{\varphi}(j) </math>, we can find our values of <math> \varphi_j </math> using the fact <math> b_j = \int_{V_{\varphi}(j)} f(x)dx </math>. Recall that <math> f(x) </math> refers to a density of the measure <math> \mu </math>, i.e., <math> \mu = f(x)dx </math>. We define the Voronoi cells with | |||
<math display="block"> V_{\varphi}(j) = \Big\{ x \in X : \forall j' \neq j, \frac{1}{2}|x-y_j|^2 - \varphi_j \leq \frac{1}{2}|x-y_{j'}|^2 - \varphi_{j'} \Big\}. </math> | |||
We use the specific cost function <math> c(x,y) = \frac{1}{2}|x-y|^2 </math> here. This is a special case and we may generalize to other cost functions if we desire. When we have this special case, the decomposition of our space <math> X </math> is known as a "power diagram."<ref name="Merigot"/> | |||
== The gradient in finding optimal <math> \varphi </math> == | |||
Finding the weights via the above method is equivalent to maximizing <math> \mathcal{E}(\varphi) </math>, and we may do this by taking the partial derivatives of this function with respect to <math> \varphi_j </math>. This is the same as taking the gradient of <math> \mathcal{E}(\varphi) </math>. In partial derivative form, we have | |||
<math display="block"> \frac{\partial \mathcal{E} }{\partial \varphi_j} = - \int_{V_{\varphi}(j)} f(x)dx + b_j </math><ref name="Merigot"/> | |||
and in gradient form, we have | |||
<math display="block"> \nabla \mathcal{E}(\varphi)_j = - \int_{V_{\varphi}(j)} f(x)dx + b_j .</math> | |||
Since <math> \nabla \mathcal{E}(\varphi)_j = 0 </math> when it attains a maximum, we have the relation between the weights and the measure density that we established in the previous section. Note that the maximum is taken and not the minimum because our function <math> \mathcal{E}(\varphi) </math> is a concave function. The mapping <math> \varphi \rightarrow \sum_j \varphi_j b_j </math> is linear, but because we consider an infimum for <math> \varphi^c </math>, the overall function <math> \mathcal{E}(\varphi) </math> is concave.<ref name="Merigot"/> | |||
= | Once we have discovered our optimal <math> \varphi_j </math>, the optimal transport map is is one in which any <math> x \in V_{\varphi_j} </math> is mapped to <math> y_j </math>. We have the mapping to a constant over each particular region, making the optimal transport map piecewise constant.<ref name="Peyré and Cuturi"/> | ||
== Algorithm discussion == | |||
We | We may search for a maximum of value of <math> \mathcal{E}(\varphi) </math> by means of certain algorithms, the first being gradient ascent. Whether or not such an algorithm is capable of being implemented effectively is contingent on the ability to find our power diagram in a practical way. Certain computational geometry<ref name="Santambrogio"/> algorithms allow the cells to be found efficiently. A second suitable algorithm is Newton's method. Using Newton's method to find the zeros of <math> \frac{\partial \mathcal{E} }{\partial \varphi_j} </math>, one must compute the second derivative of <math> \mathcal{E} </math>, as well as justify certain constraints are met, such as bounded eigenvalues of the Hessian.<ref name="Santambrogio"/> | ||
== References == | |||
<references> | |||
<ref name="Merigot">[https://arxiv.org/pdf/1803.00567.pdf Mérigot Q., ''A Multiscale Approach to Optimal Transport'', Laboratoire Jean Kuntzmann, Université de Grenoble and CNRS.]</ref> | |||
<ref name="Santambrogio">[https://link-springer-com.proxy.library.ucsb.edu:9443/content/pdf/10.1007%2F978-3-319-20828-2.pdf F. Santambrogio, ''Optimal Transport in Applied Mathematics'', Chapter 6.]</ref> | |||
<ref name="Peyré and Cuturi">[https://arxiv.org/pdf/1803.00567.pdf G. Peyré and M. Cuturi, ''Computational Optimal Transport'', Chapter 5.]</ref> | |||
</references> | |||
Latest revision as of 04:38, 28 February 2022
Semidiscrete optimal transport refers to situations in optimal transport where two input measures are considered, and one measure is a discrete measure and the other one is absolutely continuous with respect to Lebesgue measure.[1] Hence, because only one of the two measures is discrete, we arrive at the appropriate name "semidiscrete."
Formulation of the semidiscrete dual problem
In particular, we will examine semidiscrete optimal transport in the case of the dual problem. The general dual problem for continuous measures can be stated as
where denote probability measures on domains respectively, and is a cost function defined over . denotes the set of possible dual potentials, and the condition is satisfied. It should also be noted that has a density such that . Now, we would like to extend this notion of the dual problem to the semidiscrete case. Such a case can be reformulated as
Aside from using a discrete measure in place of what was originally a continuous one, there are a few other notable distinctions within this reformulation. The first is that denotes the c-transform of . The c-transform can be defined as . is used to denote . Furthermore, we note that our original measure is a sum of Dirac masses evaluated at locations with weights , i.e., .
Voronoi cells decomposition
Now, we will establish the notion of Voronoi cells. The Voronoi cells refer to a special subset of , and the reason we are interested in such a subset is because we can use the Voronoi cells to find the regions that are sent to each . In particular, if we denote the set of Voronoi cells as , we can find our values of using the fact . Recall that refers to a density of the measure , i.e., . We define the Voronoi cells with
We use the specific cost function here. This is a special case and we may generalize to other cost functions if we desire. When we have this special case, the decomposition of our space is known as a "power diagram."[3]
The gradient in finding optimal
Finding the weights via the above method is equivalent to maximizing , and we may do this by taking the partial derivatives of this function with respect to . This is the same as taking the gradient of . In partial derivative form, we have
and in gradient form, we have
Since when it attains a maximum, we have the relation between the weights and the measure density that we established in the previous section. Note that the maximum is taken and not the minimum because our function is a concave function. The mapping is linear, but because we consider an infimum for , the overall function is concave.[3]
Once we have discovered our optimal , the optimal transport map is is one in which any is mapped to . We have the mapping to a constant over each particular region, making the optimal transport map piecewise constant.[1]
Algorithm discussion
We may search for a maximum of value of by means of certain algorithms, the first being gradient ascent. Whether or not such an algorithm is capable of being implemented effectively is contingent on the ability to find our power diagram in a practical way. Certain computational geometry[2] algorithms allow the cells to be found efficiently. A second suitable algorithm is Newton's method. Using Newton's method to find the zeros of , one must compute the second derivative of , as well as justify certain constraints are met, such as bounded eigenvalues of the Hessian.[2]
































